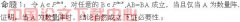对于解集非空的一元二次不等式的求解,我们常用“两根之间”、“两根之外”这类简缩语来说明其结果,同时也表明了它的解法.这是用“等”来解决“不等”的一个典型例子.从表面上看,“等”和“不等”是对立的,但如果着眼于“等”和“不等”的关系,会发现它们之间相互联系的另一面.设M、N是代数式,我们把等式M=N叫做不等式M<N,M≤N,M>N、M≥N相应的等式.我们把一个不等式与其相应的等式对比进行研究,发现“等”是“不等”的“界点”、是不等的特例,稍微深入一步,可以从“等”的解决来发现“不等”的解决思路、方法与技巧.本文通过几个常见的典型例题揭示“等”对于“不等”在问题解决上的启示.
? 1.否定特例,排除错解
?解不等式的实践告诉我们,不等式的解区间的端点是它的相应等式(方程)的解或者是它的定义区间的端点(这里我们把+∞、-∞也看作端点).因此我们可以通过端点的验证,否定特例,排除错解,获得解决问题的启示.
?例1 满足sin(x-π/4)≥1/2的x的集合是().
??A.{x|2kπ+5π/12≤x≤2kπ+13π/12,k∈Z}
??B.{x|2kπ-π/12≤x≤2kπ+7π/12,k∈Z}
??C.{x|2kπ+π/6≤x≤2kπ+5π/6,k∈Z}
??D.{x|2kπ≤x≤2kπ+π/6,k∈Z}∪{2kπ+5π/6≤(2k+1)π,k∈Z}(1991年三南试题)
?分析:当x=-π/12、x=π/6、x=0时,sin(x-π/4)<0,因此排除B、C、D,故选A.
?例2 不等式 +|x|/x≥0的解集是().
??A.{x|-2≤x≤2}
??B.{x|- ≤x<0或0<x≤2}
??C.{x|-2≤x<0或0<x≤2}
??D.{x|- ≤x<0或0<x≤ }
? 分析:由x=-2不是原不等式的解排除A、C,由x=2是原不等式的一个解排除D,故选B.
?这两道题若按部就班地解来,例1是易错题,例2有一定的运算量.上面的解法省时省力,但似有“投机取巧”之嫌.选择题给出了三误一正的答案,这是问题情景的一部分.而且是重要的一部分.我们利用“等”与“不等”之间的内在联系,把目光投向解区间的端点,化繁为简,体现了具体问题具体解决的朴素思想,这种 “投机取巧”正是抓住了问题的特征,体现了数学思维的敏捷性和数学地解决问题的机智.在解不等式的解答题中,我们可以用这种方法来探索结果、验证结果或缩小探索的范围.
?例3 解不等式loga(1-1/x)>1.(1996年全国高考试题)
?分析:原不等式相应的等式--方程loga(1-1/x)=1的解为x=1/(1-a)(a≠1是隐含条件).原不等式的定义域为(1,+∞)∪(-∞,0).当x→+∞或x→-∞时,loga(1-1/x)→0,故解区间的端点只可能是0、1或1/(1-a).当0<a<1 时,1/(1-a)>1,可猜测解区间是(1,1/(1-a));当a>1时,1/(1-a)<0,可猜测解区间是(1/(1-a),0).当然,猜测的时候要结合定义域考虑.
?上面的分析,可以作为解题的探索,也可以作为解题后的回顾与检验.如果把原题重做一遍视为检验,那么一则费时,对考试来说无实用价值,对解题实践来说也失去检验所特有的意义;二则重做一遍往往可能重蹈错误思路、错误运算程序的复辙,费时而于事无补.因此,抓住端点探索或检验不等式的解,是一条实用、有效的解决问题的思路.
?2.诱导猜想,发现思路
?当我们证明不等式M≥N(或M>N、M≤N、M<N)时,可以先考察M=N的条件,基本不等式都有等号成立的充要条件,而且这些充要条件都是若干个正变量相等,这就使我们的思考有了明确的目标,诱导猜想,从而发现证题思路.这种思想方法对于一些较难的不等式证明更能显示它的作用.
?例4 设a、b、c为正数且满足abc=1,试证:1/a3(b+c)+1/b3(c+a)+1/c3(a+b)≥3/2.(第36届IMO第二题)
?分析:容易猜想到a=b=c=1时,原不等式的等号成立,这时1/a3(b+c)=1/b3(c+a)=1/c3(a+b)=1/2.考虑到“≥”在基本不等式中表现为“和”向“积”的不等式变换,故想到给原不等式左边的每一项配上一个因式,这个因式的值当a=b=c=1时等于1/2,且能通过不等式变换的运算使原不等式的表达式得到简化.
?1/a3(b+c)+(b+c)/4bc≥ =1/a,
?1/b3(a+c)+(a+c)/4ca≥1/b,
?1/c3(a+b)+(a+b)/4ab≥1/c,
?将这三个等式相加可得
?1/a3(b+c)+1/b3(c+a)+1/c3(a+b)≥1/a+1/b+1/c-(1/4)[(b+c)/bc+(c+a)/ca+(a+b)/ab]=(1/2)(1/a+1/b+1/c)≥(3/2) =3/2,从而原不等式获证.
?这道题看似不难,当年却使参赛的412名选手中有300人得0分.上述凑等因子的思路源于由等号的成立条件而产生的猜想,使思路变得较为自然,所用的知识是一般高中生所熟知的.再举二例以说明这种方法有较大的适用范围.
?例5 设a,b,c,d是满足ab+bc+cd+da=1的正实数,求证:a3/(b+c+d)+b3/(a+c+d)+c3/(a+b+d)+d3/(a+b+c)≥1/3.(第31届IMO备选题)
?证明:a3/(b+c+d)+a(b+c+d)/9≥(2/3)a2,
?b3/(a+c+d)+b(a+c+d)/9≥(2/3)b2,
?c3/(a+b+d)+c(a+b+d)/9≥(2/3)c2,
?d3/(a+b+c)+d(a+b+c)/9≥(2/3)d2.
?∴ a3/(b+c+d)+b3/(a+c+d)+c3/(a+b+d)+d3/(a+b+c)≥(2/3)(a2+b2+c2+d2)-(2/9)(ab+bc+cd+da+ac+bd)
?=(5/9)(a2+b2+c2+d2)-(2/9)(ab+bc+cd+da)+(1/9)(a2+c2-2ac+b2+d2-2bd)
?≥(5/9)(a2+b2+c2+d2)-(2/9)(ab+bc+cd+da)≥(5/9)(ab+bc+cd+da)-(2/9)(ab+bc+cd+da)=(1/3)(ab+bc+cd+da)=1/3.
?当a=b=c=d=1/2时,原不等式左边的四个项都等于1/12,由此出发凑“等因子”.对于某些中学数学中的常见问题也可用这种方法解决,降低问题解决对知识的要求.
?例6 设a,b,c,d∈R+,a+b+c+d=8,求M= + + + 的最大值.
?分析:猜想当a=b=c=d=2时M取得最大值,这时M中的4个项都等于3.要求M的最大值,需将M向“≤”的方向进行不等变换,由此可得 3 ≤(3+4a+1)/2=2a+2,3 ≤2b+2,3 ≤2c+2,3 ≤2d+2.于是3M≤2(a+b+c+d)+8=24,∴M≤8.当且仅当a=b=c=d时等号成立,所以M的最大值为8.
?当然,例6利用平方平均数不小于算术平均数是易于求解的,但需要高中数学教材外的知识.利用较少的知识解决较多的问题,是数学自身的追求,而且从教学上考虑,可以更好地培养学生的数学能力.先有猜想,后有设计,再有证法,也是数学地思考问题的基本特征.
?3.引发矛盾,启迪探索
?在利用基本不等式求最大值或最小值时,都必须考虑等号能否取得,这不仅是解题的规范要求,而且往往对问题的解决提供有益的启示.特别当解题的过程似乎顺理成章,但等号成立的条件却发生矛盾或并不一定成立.这一新的问题情景将启迪我们对问题的进一步探索.
?例7 设a,b∈R+,2a+b=1,则2 -4a2-b2有().
??A.最大值1/4? B.最小值1/4
??C.最大值( -1)/2? D.最小值( -1)/2
? 分析:由4a2+b2≥4ab,得原式≤2 -4ab=-4( )2+2 =-4( -1/4)2+1/4≤1/4.若不对不等变换中等号成立的条件进行研究,似已完成解题任务,而且觉得解题过程颇为自然,但若研究一下等号成立的条件,则出现了矛盾:要使4a2+b2≥4ab中的等号成立,则应有 2a=b=1/2,这时 = /4≠1/4,第二个“≤”中的等号不能成立.这一矛盾使我们感觉到解题过程的错误,促使我们另辟解题途径.事实上,原式=2 -(2a+b)2+4ab=4ab+2 -1,而由1=2a+b≥2 得0< ≤ /4,ab≤1/8,∴原式≤ /2+1/2-1=( -1)/2,故选?C